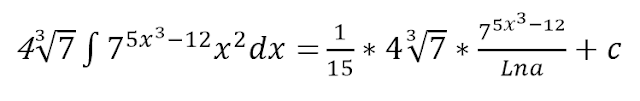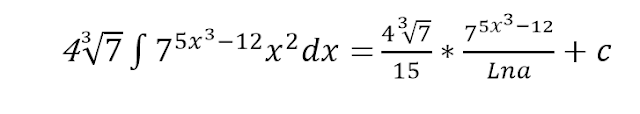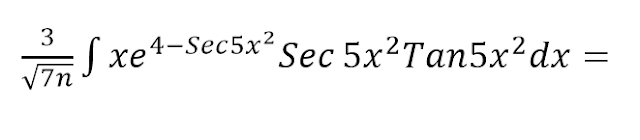Operación inversa del calculo diferencial, que se emplea para calcular, entre otras cosas, el área bajo una curva y el eje x, con fronteras definidas a la izquierda y a la derecha, a las que se les denomina intervalo.
Observe la figura 1
Fig. 1
El área sombreada en la Fig. 1, comprendida bajo la curva definida por la función f(x), el eje x y los limites inferior a, e inferior b, se calcula con la formula:
Área= Base*Altura (1)
en la que la Base=b-a y la Altura se da por el valor de la función en el punto b, lo que se expresa por f(b).
Sustituyendo en (1) estas expresiones
Área=(b-a)*f(b) (2)
Observe que el Área calculada de esta forma es imprecisa, debido a el lado irregular que se da por el segmento superior de la curva. Esto ocaciona que se incluyan en el calculo [hechos con la expresión (2)], en algunos sectores, porciones de área que no están bajo la curva, y en algunos otros sectores, estas porciones de área se se excluyen.Este hecho se observa en la fig. 2.
En este gráfico se nota que el área A1 se esta excluyendo en el calculo del área total, a pesar de que es una porción de área que esta bajo la curva. Vea que lo contrario pasa con el A2, la cual se esta incluyendo en el calculo, a pesar de que esta no esta bajo la curva. Este hecho es el que causa errores en el calculo de un área bajo la curva.
La manera de minimizar el error al máximo, para calcular el área bajo una curva, es el dividir esta área, en una infinidad de rectángulos infinitamente pequeños, y posteriormente sumar cada una de sus áreas, empleando una técnica llamada Suma de Riemann, la cual, posteriormente se discutirá.
Note este hecho en la siguiente figura
Suponiendo que el área mostrada en lFig. 3, se subdividió en una infinidad de rectángulos, y cada uno de estos es infinitamente pequeño, procedemos a estimar su expresión o formula.
El área Total se calcula
La Altura para cada rectángulo en la Fig. 3 se da por el valor de la función en el punto donde el rectángulo intersecta la curva, A saber:
La base para cada rectángulo en esta misma figura sera:
Sustituyendo en (3) las expresiones de las bases y las alturas
Sin, embargo, recordemos que el área se subdividió en rectángulos de bases iguales, por lo que la expresión (4) la podemos escribir como
La manera de minimizar el error al máximo, para calcular el área bajo una curva, es el dividir esta área, en una infinidad de rectángulos infinitamente pequeños, y posteriormente sumar cada una de sus áreas, empleando una técnica llamada Suma de Riemann, la cual, posteriormente se discutirá.
Note este hecho en la siguiente figura
Fig. 3
El área Total se calcula
AT=A1 + A2 +...+ An-1 +An (3)
La base para cada rectángulo en esta misma figura sera:
Sustituyendo en (3) las expresiones de las bases y las alturas
Sin, embargo, recordemos que el área se subdividió en rectángulos de bases iguales, por lo que la expresión (4) la podemos escribir como
la cual se lee: el área total es igual al limite de la sumatoria de todas las áreas desde k=1 hasta n, cuando n tiende hasta infinito.
Empleando la notación de Leibniz, la expresión anterior quedaría
Anteriormente mencionamos que El calculo integral se emplea para calcular Áreas bajo una curva. Una curva, esta representada por una función, o expresión matemática determinada. Por otro lado, sabemos que hay una gran cantidad y variedad de funciones distintas, esto trae como consecuencia que se tengan que emplear diferentes formulas para poder integrar estas funciones. Se crearon diferentes formulas de integración, cada una de ellas se emplea para integrar un tipo de función especifica, las cuales se trataran enseguida.
EJERCICIOS RESUELTOS
Esta formula se emplea para integrar una función, a la que igualaremos con v, y que esta afectada con un exponente n. Pero observe que al lado derecho de v, se encuentra dv. Esto significa que para poder integrar una función de esta naturaleza, al derivar la función representada por v, debemos lograr como derivada, la expresión que este a un lado de mencionada función. Por lo tanto a la expresión dv que aparece en la formula, le llamaremos condición. Esta condición se debe cumplir, para poder integrar tal como lo indica la formula
INTEGRACIÓN DE UNA CONSTANTE QUE ESTA AFECTADA CON UN EXPONENTE VARIABLE
(INTEGRAL TRASCENDENTE)
(INTEGRAL TRASCENDENTE)
La fórmula para integrar una constante
que tiene como exponente un término variable o un polinomio es
EJERCICIOS RESUELTOS
Por analogía
a la formula
v=x
y al derivar
se logra
dv=1dx
y se observa
que la derivada obtenida es igual a la expresión que está a un lado de
, por lo que se cumple la condición que
plantea la formula en cuestión, por lo tanto el resultado es el que esta misma
presenta, esto es
En la que se
arrastra el 6, tal como lo dan en el problema, o sea, multiplicando.
En este problema el
exponente variable es 4x-4, por lo tanto
V=4x-6
Según lo indica la
fórmula que estamos empleando. Ahora derivamos para ver si se cumple la
condición que está a un lado de
En este problema el
exponente variable es 4x-4, por lo tanto
V=4x-6
Según lo indica la fórmula
que estamos empleando. Ahora derivamos para ver si se cumple la condición que
está a un lado de
.
dv=4dx
Observe que la condición si se cumple, ya que a
un lado de
esta
dx que es lo que se obtuvo al derivar. El 4 que aparece con dx, y que no está
en la expresión a integrar, solo se compensa con su inverso multiplicativo que es ¼,
introduciéndolo en el resultado, multiplicando. Veamos
En este problema vemos que
Y su derivada es
Vemos que la
expresión
es igual a la que está a un lado
de
salvo el 15 que se obtuvo en el proceso de derivación, pero como sabemos
que se admiten diferencias cuando estas son valores constantes, podemos decir
que si se cumple la condición que señala la formula, solo debemos compensar el 15. Veamos
El termino
El resultado definitivo será
Resolvamos el problema
Efectuando
operaciones
Se nota que la derivada obtenida es igual a la
expresión que está a un lado de
Por ello concluimos que la condición se cumple,
solo compensamos el 16/3. Veamos el proceso
INTEGRACIÓN DE LA CONSTANTE e AFECTADA CON UN EXPONENTE VARIABLE(INTEGRAL TRASCENDENTE)
La formula empleada para este caso particular es
Obtenga el resultado de las siguientes
integrales
Sabemos que el
exponente es el que se iguala a v, según la fórmula que estamos tratando, de
forma que
Expresión,
que al compararla con aquella que está enfrente deL temino
en
la integral a resolver , concluimos que son iguales, salvo el -5/4 que se debe
compensar en el resultado de la integral, con el inverso multiplicativo. El
coeficiente que esta tiene
Por analogía a la formula en cuestión igualamos
el exponente de la e con
v, esto es;
Se nota que esta expresión obtenida al
derivar, es igual a la expresión que esta alrededor de e y su exponente
,
condición que presenta la fórmula que
estamos viendo, por
ello concluimos que este problema si se puede resolver con
esta fórmula. Arrastrando el coeficiente y compensando el
10;
PROBLEMAS PROPUESTOS
INTEGRACIÓN DE FUNCIONES TRIGONOMÉTRICAS
















































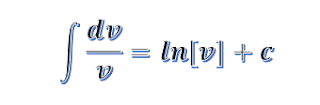

.PNG)